How do I predict Time Series
시계열 데이터란 무엇인가
시계열 데이터는 연속적인 시간 주기 동안에 관찰된 다수의 데이터
- Variable : 시간이 지남에 따라 변화는 것
- Time Periods : 매일, 주마다, 월별, 년별 등..
- Variable Behaviour : 정량화(quantifiable)할 수 있는 값
Past Is Important
대부분의 시계열 데이터는 과거의 값에 의존적임
가장 최근에 위치한 과거의 값은 variable’s behabiour를 잘 나타냄
한 개의 변수의 Lagged values는 하나 혹은 더 많은 값에 대해 현재 그리고 미래 예측을 위해 회귀함
결측치는 자주 과거데이터로 채워짐
데이터간의 상호관계는 미래 시간의 포인트를 예측하는 모델에 공식화됨
현재 그리고 미래의 가중합은 미래 데이터를 예측함
Role of Lag Operator
Lag Operator는 모델이 과거,현재 그리고 미래의 데이터가 서로서로 연관 되었는지를 수치화할 수 있게 해줌
Past can be used to predict future. Some time series data is totally random.
과거, 현재 미래 데이터 들은 회귀분석 기술을 이용해 모델화 될 수 있음
Y(at Time T) = Intercept x Exponential ^(rate of growth at time T)
- Y : 예측값
- Intercept : x축을 시간, y축을 실제 값이라고 했을때 시간이 0일 때의 y 값임
Linear Vs Non-Linear Time Series
- Linear time series
- 트렌드가 직선적임
- 일정한 gradient(growth/decay)를 가짐
- Non-Linear time series
- 곡선적인 trend 라인을 가짐
- 트렌드가 기하급수적이거나 시간에 대해 원2차적임(time quadratic)
Non Linear Time Series To Linear Time Series
비선형 시계열 데이터는 log를 취함으로써 선형 시계열 데이터가 될 수 있음
ln(Y at time T) = ln(Intercept) x Rate of growth at time T
Deterministic Vs Non-Deterministic Time Series
Deterministic Time Series는 항상 예상되는 방향으로 움직임
Non-deterministic Time Series는 stocahstic 또는 random 함
시계열 데이터를 이해하기 위해서 평균(expected value), 분산(variance), 공분산(covariance),상관관계(correlation) 등이 필요함
Covariance Stationary Time Series
시계열 모델을 예측하기 위해서는 covariance stationary를 보장하는 것이 중요함
If a time series mean, variance and covariance with past and future values do not change over time then the model is known to be covariance stationary.
Benefits Of Covariance Stationary(안정적) Models
안정적인 시계열 모델들은 신뢰 가능하고 좀 더 잘 데이터를 추정 가능하게 함
더 좋은 예측을 하기 위해서 시계열 데이터는 안정적인 상태가 되어야함
안정적인 상태는 시계열 데이터가 다른 시간 포인트들 간에 어떠한 숨겨진 연관성이 없어야 하고 움직임은 고정적인 것
백색잡음(White noise)는 시계열 데이터가 0인 평균, 일정한 분산 그리고 데이터 포인트들 간의 다수의 상관관계가 없는 과정임
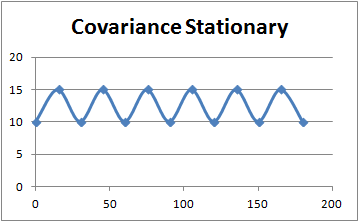
3 Criteria Of Time Series Covariance Stationary
시계열 데이터는 다음 아래 3가지 기준을 만족해야 안정적이라 할 수 있음
1. Constant Mean
시계열의 평균 혹은 기대값 연속적인 시간 선상 안에서 일정해야함
How do I check if expected value (mean) is changing in a time series?
시계열 평균이 일정한지 확인하기 위해서는 시간을 일정 구간의 셋으로 분리하고 각 셋의 합의 평균을 구하면 가능
- The calculated mean of each set should be constant.
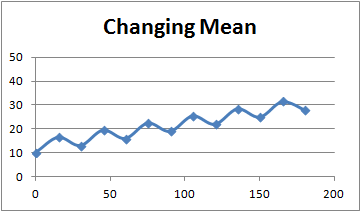
How does a changing mean time series look?
시계열 평균이 시간에 의존적이라면 증가 트렌드를 가짐
2. Constant Variance
시계열의 분산 혹은 표준편차 시간에 대해서 일정 해야하며 시간에 의존성이 없어야함
How do I check if variance is changing in a time series?
시계열 분산이 일정한지 확인하기 위해서는 시간을 일정 구간의 셋으로 분리하고 분산을 구하는 연산을 수행
분산은 처음에는 각 실측과 평균의 차이를 가지고 마지막으로 차이를 합친 다음에 전체 차이를 구간 안에는 모든 측정치의 개수로 나눈 값에 의해 계산됨
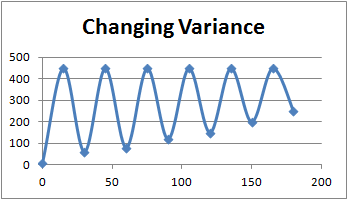
How does a changing variance time series look?
다음 그림은 시간에 따라 분산(variance)가 바뀌는 것을 보여줌
3. Constant Covariance
공분산(covariance)를 이해하기 위해 상관관계를 이해함이 중요
상관관계(Correlation)은 변수들 사이의 같은 움직임(co-movemet) 관계가 얼마나 강한지 측정함
상관관계는 두 개의 변수의 표준화된 분산임
Covariance(X,Y) At Time Point T = Expected Value of (X, Y) — ((Std of X) x (Std of Y) for each
How do I check if covariance is changing in a time series?
두 개의 연속적인 포인트에 대해서 공분산을 구해 나가면서 시간에 dependnet가 있는지 확인
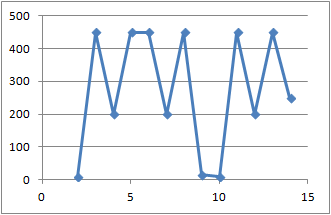
How does changing covariance time series look?
공분산이 일정하지 않으면 시계열 데이터는 랜덤성(명백한 패턴 없이 시계열 데이터가 바뀜)을 보임
이 같은 패턴을 hetroscedasticity 으로 함
Seasonality
패턴의 반복을 시계열 데이터에서 관찰한다면 계절성이 존재함을 나타냄
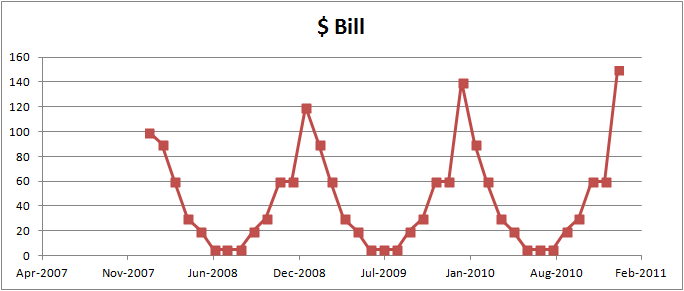
If Trend Exists => Time Series Is Not Stationary
How Do We Eliminate Seasonality
때때로 계절성에 대해 시계열을 조정하는 것은 적합하지 않음
시간 흐름의 모든 추세와 변화를 포착하는 것이 중요 할 때 특히, 계절성을 위해 시계열을 조정하는 것이 적절하지 않은 경우가 있음
그러나 오직 비계절적인 요소 만을 분석하고 싶을 때는 계절성을 조정해야함
계절성을 조정하는 방법은 차분을 하거나 평균을 취해서 계절성을 제거할 수 있음
1. Differencing-Seasonality adjusted time series
- 계절성이 보이는 시계열 포인트에 대해 각 계절성의 포인트 들을 차분
2. Regression analysis with seasonal dummy variables
- 더미 변수는 0 에서 1 까지의 값을 취하는데 여기서 0은 특정 시계열 데이터의 계절성을 무시한다는 의미
- 계절적 더미 변수들은 특수일을 설명하는 것에 쓰일 수 있음